Big-O Notation
Big-O is a framework for measuring the efficiency of an algorithm.
Why bother?
Big-O notation is used to describe the worst-case time complexity of an algorithm, so we can compare different algorithms and data structures and better predict their behavior as our input size increases.
Types of Analysis
To be able to analyze a given algorithm, we need to know which inputs take less time, and which take longer time.
Complexity cases
- Worst case
- Algorithm runs the slowest with the given input
- Best case
- Algorithm runs the fastest with the given input
- Avergae case
- Assumes input is random
- Run the algorithm many times with different inputs
Performance measuring
- Time complexity
- Amount of time taken to perform the task
- Space complexity
- Amount of memory needed to perform the task
Asymptotic Analysis
Asymptotic analysis is a method used to describe the limiting behaviour of a function or algorithm as its argument approaches a particular value or infinity. It is input bound, all other factors are considered constant.
Grow rate functions
With the analysis theory out of our way, we need to look at a way to describe the behavior of algorithms while the input gets larger. This relation is called the growth rate.
Common growth rates
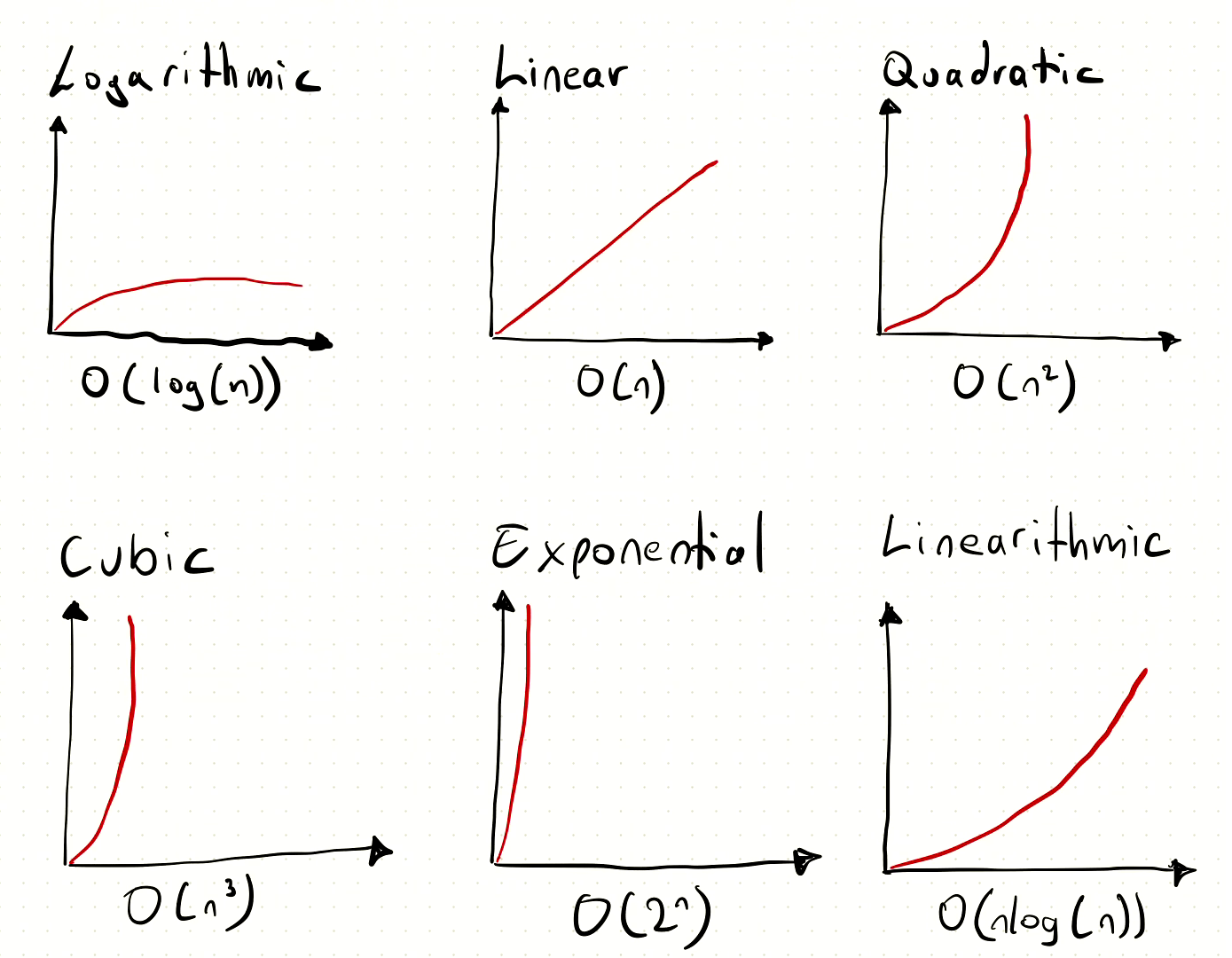
The king of kings
But there is also Constant Function: O(1) - which value doesn’t change with input size.
Examples
| Complexity | Name | Example |
|---|---|---|
| 1 | Constant | Adding an element to the front of a linked list |
| logn | Logarithmic | Finding an element in a sorted array |
| n | Linear | Finding an element in an unsorted array |
| nlogn | Linear Logarithmic | Sorting n items by ‘divide-and-conquer’-Mergesort |
| n2 | Quadratic | Shortest path between two nodes in a graph |
| n3 | Cubic | Matrix Multiplication |
| 2n | Exponential | The Towers of Hanoi problem |
Conclusion
While we can’t always have O(1) it is important to know how costly our implementations are to be able to predict/prevent possible bottlenecks in our applications or refactor slow-performing code.